Topic Modeling with Amortized LDA

In this tutorial, we will explore how to run the amortized Latent Dirichlet Allocation (LDA) model implementation in scvi-tools. LDA is a topic modelling method first introduced in the natural language processing field. By treating each cell as a document and each gene expression count as a word, we can carry over the method to the single-cell biology field.

Below, we will train the model over a dataset, plot the topics over a UMAP of the reference set, and inspect the topics for characteristic gene sets.

As an example, we use the PBMC 10K dataset from 10x Genomics.

Note

Running the following cell will install tutorial dependencies on Google Colab only. It will have no effect on environments other than Google Colab.

!pip install --quiet scvi-colab
from scvi_colab import install

install()

WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv

import os
import tempfile

import pandas as pd
import scanpy as sc
import scvi
import seaborn as sns
import torch

scvi.settings.seed = 0
print("Last run with scvi-tools version:", scvi.__version__)

Last run with scvi-tools version: 1.1.0

Note

You can modify save_dir below to change where the data files for this tutorial are saved.

sc.set_figure_params(figsize=(6, 6), frameon=False)
sns.set_theme()
torch.set_float32_matmul_precision("high")
save_dir = tempfile.TemporaryDirectory()

%config InlineBackend.print_figure_kwargs={"facecolor": "w"}
%config InlineBackend.figure_format="retina"

Load and process data

Load the 10x genomics PBMC dataset. Generally, it is good practice for LDA to remove ubiquitous genes, to prevent the model from modeling these genes as a separate topic. Here, we first filter out all mitochrondrial genes, then select the top 1000 variable genes with seurat_v3 method from the remaining genes.

adata_path = os.path.join(save_dir.name, "pbmc_10k_protein_v3.h5ad")
adata = sc.read(
    adata_path,
    backup_url="https://github.com/YosefLab/scVI-data/raw/master/pbmc_10k_protein_v3.h5ad?raw=true",
)

adata.layers["counts"] = adata.X.copy()  # preserve counts
sc.pp.normalize_total(adata, target_sum=10e4)
sc.pp.log1p(adata)
adata.raw = adata  # freeze the state in `.raw`

adata = adata[:, ~adata.var_names.str.startswith("MT-")]
sc.pp.highly_variable_genes(
    adata, flavor="seurat_v3", layer="counts", n_top_genes=1000, subset=True
)

Create and fit AmortizedLDA model

Here, we initialize and fit an AmortizedLDA model on the dataset. We pick 10 topics to model in this case.

n_topics = 10

scvi.model.AmortizedLDA.setup_anndata(adata, layer="counts")
model = scvi.model.AmortizedLDA(adata, n_topics=n_topics)

Note

By default we train with KL annealing which means the effective loss will generally not decrease steadily in the beginning. Our Pyro implementations present this train loss term as the elbo_train in the progress bar which is misleading. We plan on correcting this in the future.

model.train()

Epoch 1000/1000: 100%|██████████| 1000/1000 [05:55<00:00,  2.82it/s, v_num=1, elbo_train=1.85e+7]

Visualizing learned topics

By calling model.get_latent_representation(), the model will compute a Monte Carlo estimate of the topic proportions for each cell. Since we use a logistic-Normal distribution to approximate the Dirichlet distribution, the model cannot compute the analytic mean. The number of samples used to compute the latent representation can be configured with the optional argument n_samples.

topic_prop = model.get_latent_representation()
topic_prop.head()

	topic_0	topic_1	topic_2	topic_3	topic_4	topic_5	topic_6	topic_7	topic_8	topic_9
index
AAACCCAAGATTGTGA-1	0.000231	0.001881	0.727143	0.000329	0.200861	0.068336	0.000789	0.000109	0.000099	0.000223
AAACCCACATCGGTTA-1	0.001669	0.001529	0.917919	0.000259	0.004995	0.067332	0.005908	0.000156	0.000094	0.000140
AAACCCAGTACCGCGT-1	0.002555	0.000918	0.488677	0.002118	0.440468	0.055199	0.005976	0.000576	0.002724	0.000791
AAACCCAGTATCGAAA-1	0.001183	0.002146	0.001114	0.002859	0.001741	0.001102	0.001404	0.001622	0.008588	0.978241
AAACCCAGTCGTCATA-1	0.001145	0.000260	0.000225	0.000277	0.000368	0.000207	0.003037	0.000108	0.000537	0.993837

# Save topic proportions in obsm and obs columns.
adata.obsm["X_LDA"] = topic_prop
for i in range(n_topics):
    adata.obs[f"LDA_topic_{i}"] = topic_prop[[f"topic_{i}"]]

Plot UMAP

sc.tl.pca(adata, svd_solver="arpack")
sc.pp.neighbors(adata, n_pcs=30, n_neighbors=20)
sc.tl.umap(adata)
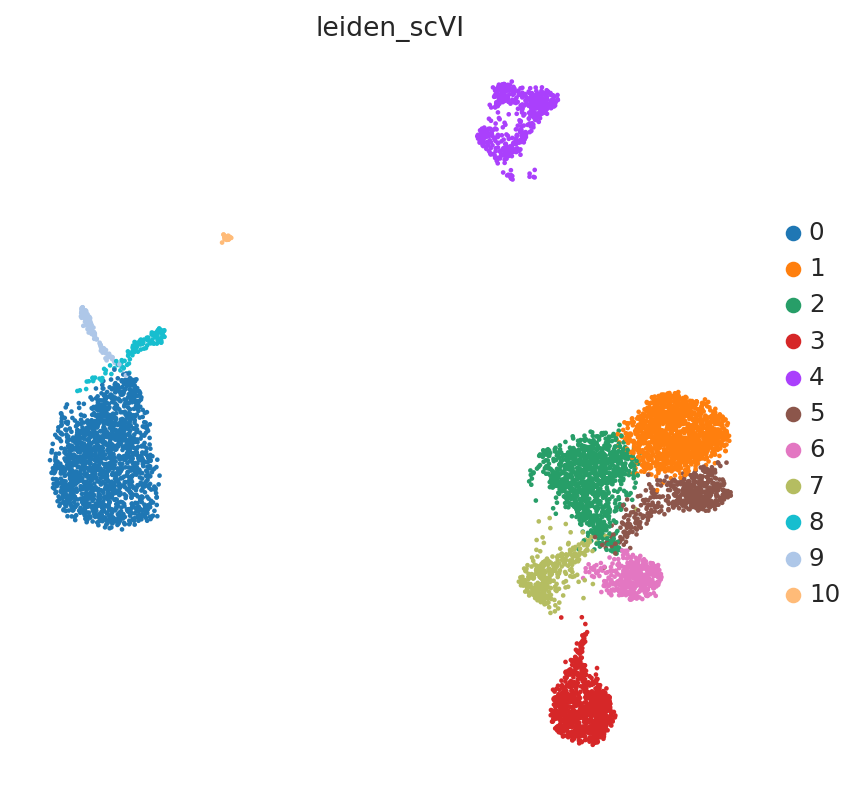
sc.tl.leiden(adata, key_added="leiden_scVI", resolution=0.8)

# Save UMAP to custom .obsm field.
adata.obsm["raw_counts_umap"] = adata.obsm["X_umap"].copy()

sc.pl.embedding(adata, "raw_counts_umap", color=["leiden_scVI"], frameon=False)

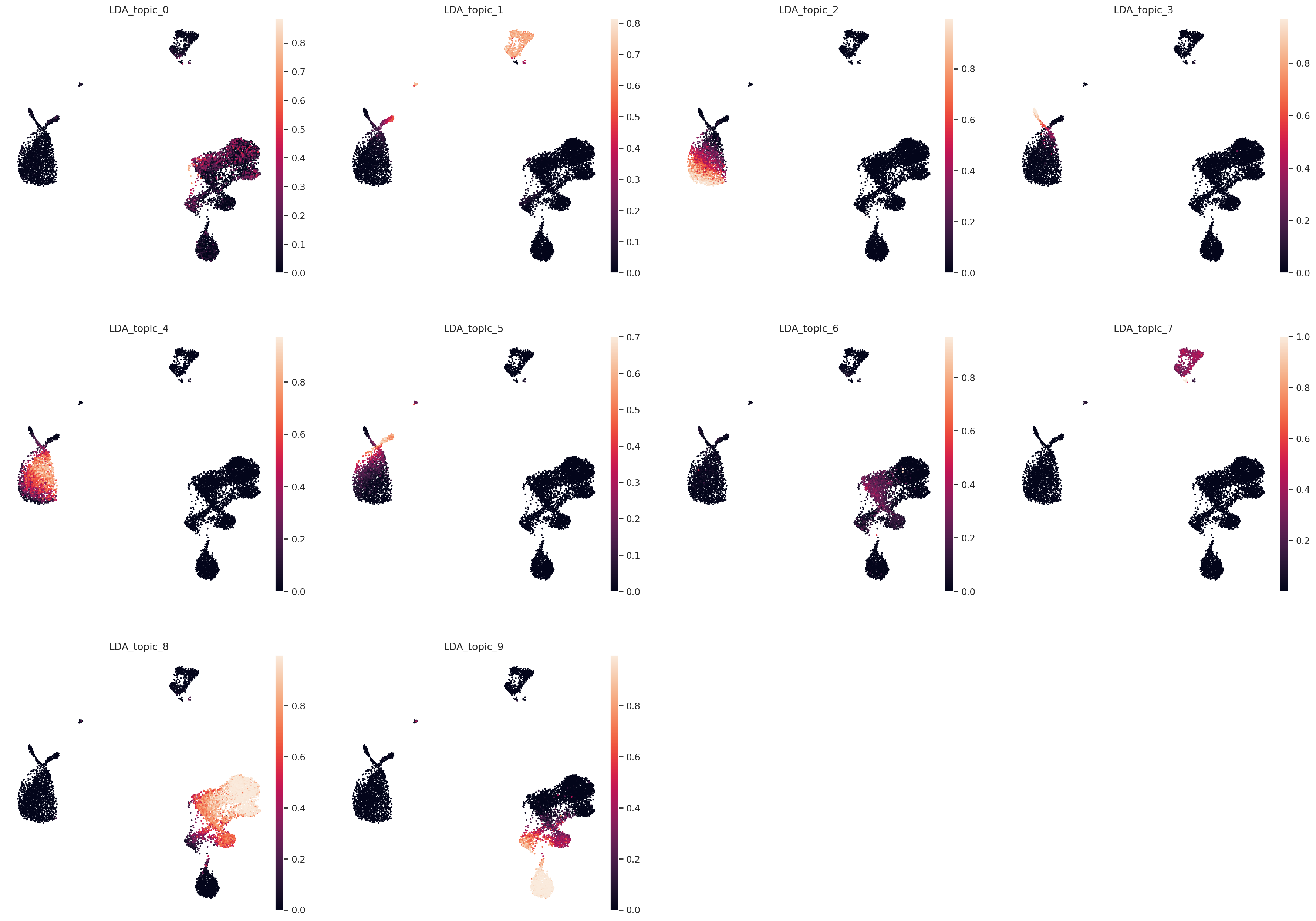
Color UMAP by topic proportions

By coloring by UMAP by topic proportions, we find that the learned topics are generally dominant in cells close together in the UMAP space. In some cases, a topic is dominant in multiple clusters in the UMAP, which indicates similarilty between these clusters despite being far apart in the plot. This is not surprising considering that UMAP does not preserve local relationships beyond a certain threshold.

sc.pl.embedding(
    adata,
    "raw_counts_umap",
    color=[f"LDA_topic_{i}" for i in range(n_topics)],
    frameon=False,
)

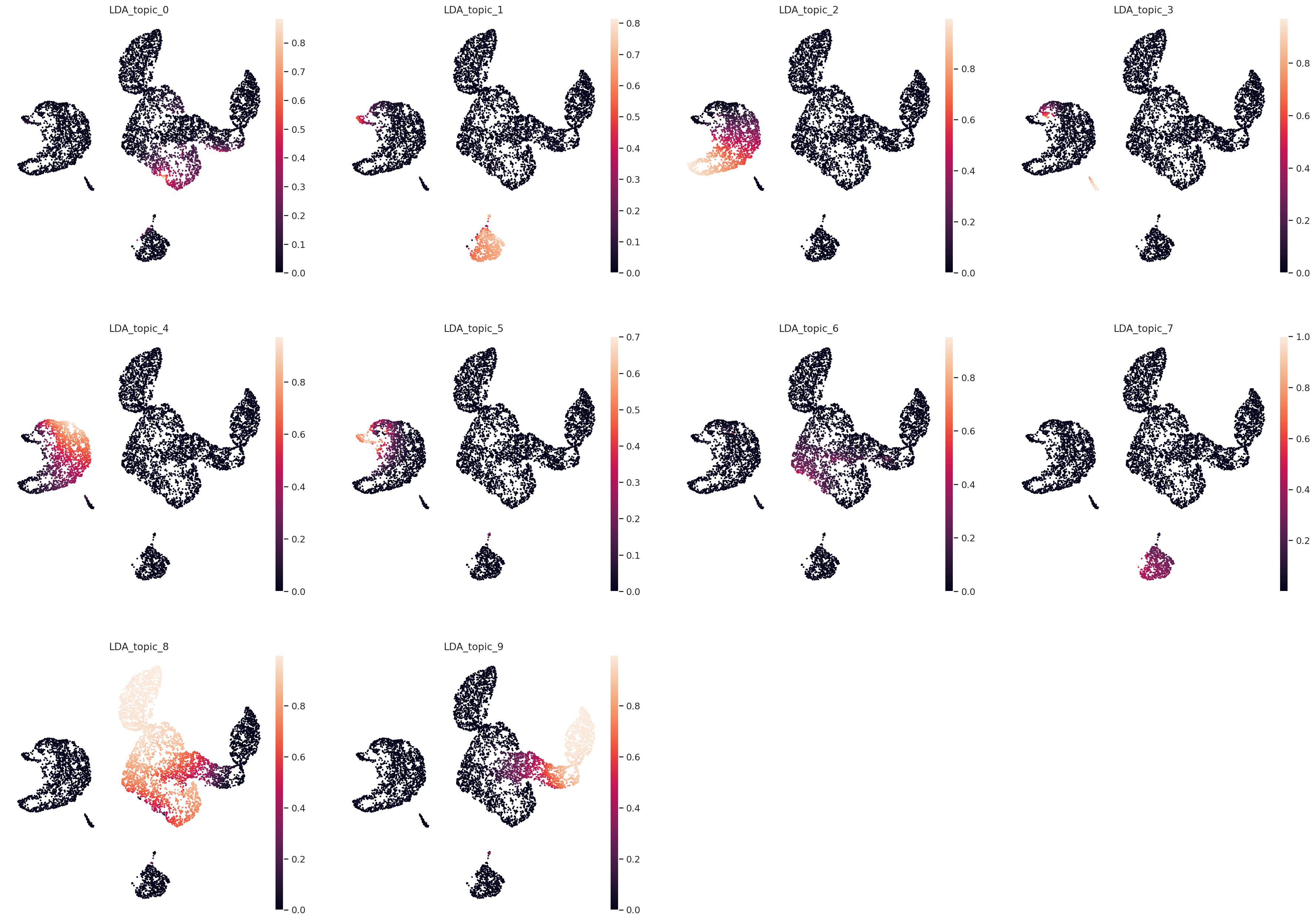
Plot UMAP in topic space

sc.pp.neighbors(adata, use_rep="X_LDA", n_neighbors=20, metric="hellinger")
sc.tl.umap(adata)

# Save UMAP to custom .obsm field.
adata.obsm["topic_space_umap"] = adata.obsm["X_umap"].copy()

sc.pl.embedding(
    adata,
    "topic_space_umap",
    color=[f"LDA_topic_{i}" for i in range(n_topics)],
    frameon=False,
)

Find top genes per topic

Similar to the topic proportions, model.get_feature_by_topic() returns a Monte Carlo estimate of the gene by topic matrix, which contains the proportion that a gene is weighted in each topic. This is also due to another approximation of the Dirichlet with a logistic-Normal distribution. We can inspect each topic in this matrix and sort by proportion allocated to each gene to determine top genes characterizing each topic.

feature_by_topic = model.get_feature_by_topic()
feature_by_topic.head()

	topic_0	topic_1	topic_2	topic_3	topic_4	topic_5	topic_6	topic_7	topic_8	topic_9
index
AL645608.8	0.000006	0.000003	3.027680e-06	0.000034	0.000001	0.000002	0.000007	0.000005	0.000001	0.000002
HES4	0.000008	0.000011	8.718006e-06	0.000709	0.000006	0.000010	0.000010	0.000009	0.000007	0.000006
ISG15	0.001584	0.000601	2.445053e-04	0.000691	0.000517	0.000033	0.000722	0.000200	0.001182	0.001377
TNFRSF18	0.000038	0.000006	7.943196e-07	0.000003	0.000001	0.000002	0.000180	0.000038	0.000403	0.000133
TNFRSF4	0.000033	0.000005	1.389031e-06	0.000004	0.000001	0.000004	0.000242	0.000008	0.000869	0.000057

rank_by_topic = pd.DataFrame()
for i in range(n_topics):
    topic_name = f"topic_{i}"
    topic = feature_by_topic[topic_name].sort_values(ascending=False)
    rank_by_topic[topic_name] = topic.index
    rank_by_topic[f"{topic_name}_prop"] = topic.values

rank_by_topic.head()

	topic_0	topic_0_prop	topic_1	topic_1_prop	topic_2	topic_2_prop	topic_3	topic_3_prop	topic_4	topic_4_prop	topic_5	topic_5_prop	topic_6	topic_6_prop	topic_7	topic_7_prop	topic_8	topic_8_prop	topic_9	topic_9_prop
0	ACTB	0.305104	CD74	0.155522	S100A9	0.150716	FTL	0.116765	FTH1	0.062567	LYZ	0.072431	S100A4	0.177341	IGKC	0.235671	TMSB4X	0.133637	TMSB4X	0.087130
1	TMSB4X	0.151037	HLA-DRA	0.095580	S100A8	0.104741	ACTB	0.067006	FTL	0.059633	ACTB	0.069452	VIM	0.052818	IGLC2	0.128583	TMSB10	0.091962	ACTB	0.085563
2	TMSB10	0.108730	TMSB4X	0.062553	LYZ	0.058034	FTH1	0.059872	LYZ	0.052926	HLA-DRA	0.050705	SH3BGRL3	0.047343	IGHA1	0.083414	ACTB	0.077558	GNLY	0.070730
3	ACTG1	0.098599	HLA-DRB1	0.055460	FTL	0.043069	TMSB4X	0.059606	TMSB4X	0.036079	CST3	0.047043	S100A10	0.043081	IGHM	0.057858	JUNB	0.038246	NKG7	0.053820
4	GAPDH	0.031823	TMSB10	0.042600	ACTB	0.038379	S100A4	0.026248	ACTB	0.031729	HLA-DRB1	0.030375	S100A6	0.042836	IGLC3	0.038808	FTL	0.030914	CCL5	0.041400